3 Chapter 3: Sampling Methods

In This Chapter You Will Learn

About the process of sampling and why it is important to the research process

The difference between a sample and a population

That there are two general types of samples—probability and non-probability samples

About the difference between probability and non-probability samples

About important concepts related to sampling, such as representativeness and generalizability

About basic procedures in drawing a sample

That random selection is a key component in probability samples

That the type of sampling required in a research study is highly related to the research question of interest

Introduction

The case study highlighted above provides one example of how sampling can be utilized in a research study. While not all studies require sampling, in those that do, sampling is a critical consideration in evaluating the results of the study. And when the sampling process breaks down in some way, it can seriously impact the results. It is therefore critical that research consumers have specific knowledge about sampling, including but not limited to the different types of sampling and problems that may directly or indirectly be associated with sampling. The goal of this chapter is to provide that critical insight.

Chapter 3 begins by examining several areas relevant to sampling. This section includes a focus on what sampling is and why researchers typically utilize a sample instead of an entire population. It then discusses the importance of randomness to the sampling process. Although random sampling is not always desired or needed in every research study that must utilize a form of sampling, it is a critical part of many research studies. This section then examines two additional areas relevant to sampling. These areas include the key concepts of representativeness and generalizability, and a brief discussion about sample size and sampling error.

The second section of this chapter examines different types of sampling methods known as probability sampling methods. Although probability sampling methods each have their own distinct features, the consistent link between all of them is that each member of a particular population has an equal chance at being selected for the sample. When researchers are interested in generalizing or applying the research results obtained from the sample to the larger population from which it was drawn (such as in the highlighted study beginning this chapter), probability samples are superior.

Chapter 3 then explores non-probability sampling methods. As opposed to probability sampling methods, non-probability sampling methods do not ensure that every member of a particular population has an equal chance at being selected for the sample. There are various situations in which a non-probability sample may be utilized and be appropriate for a particular research study. Although the various non-probability samples are unique and useful in their own way, the consistent theme among non-probability samples is that the results produced from studies utilizing this form of sampling do not generalize to a larger population. This is because not everyone in the larger population had an equal chance at being selected for the research study.

What is Sampling?

Generally, sampling refers to a process of selecting a smaller group from a larger group “in the hope that studying this smaller group (the sample) will reveal important things about the larger group (the population).”⁴ In some forms of sampling, such as probability sampling, the goal is that the smaller sample is representative of the larger population. For example, officials at your university might select a random sample of criminal justice students and ask their opinion on whether students should have the right to carry weapons on campus. In selecting a sample randomly, university officials’ goal is that the results obtained from the sample of students would be similar to the results obtained if all criminal justice students (the population) were asked their opinion on this topic. If the randomly drawn sample is representative of the population, the opinion results obtained from the sample of criminal justice students can then inform about the opinions of the entire population.

It is noteworthy to consider that sampling is certainly not limited to the social sciences. Indeed, smaller subsets of larger populations are taken in any number of scientific contexts so that researchers might learn things about some larger population. Consider environmental researchers who take core samples from glaciers in Antarctica. Environmental researchers drill deep into the glaciers with hollowed tubes to take core samples of snow and ice that have been compressed over many years. The resulting core samples are then analyzed to gather data in such areas as temperature change and atmospheric conditions over the age of the frozen core samples. Or consider beer brew masters. Brew masters also engage in a process where once a beer batch has fermented and is processed, they take a sample from the massive swirling vats of beer to determine whether the smaller sample (small glass of beer) passes muster. In essence, the small glass of beer serves as a sample of knowledge about how the larger vat of beer (or the population) might taste. The examples above also demonstrate that samples and populations need not be animate objects—samples can be produced from any number of different populations.

In both instances above, researchers as drillers or brew masters are interested in getting a smaller but representative sample of a larger population. Because these researchers are concerned with representativeness, their techniques are in ways variants of probability sampling. For example, the brew master wants to be able to generalize or apply the results of the sample beer to the larger vat of beer. Provided the sample was drawn in a way that makes it representative of the larger vat of beer, such a process negates the need for the brew master to drink hundreds and hundreds of gallons of beer to determine the quality of the batch! In many forms of sampling, especially forms of probability sampling, the nature of the sampling process allows the researcher to take a smaller but representative sample of a larger population of individuals and retrieve results that would be similar as if he or she had utilized the larger population.

Uses of Sampling

Sampling methods can be used in any number of the different research designs that are discussed in Chapters 4–6 of this text. For example, sampling can first be used to retrieve a small representative subset of individuals from a larger population. These individuals might then be randomly assigned to experimental and control groups in an experimental design as discussed in Chapter 5. Sampling can also be used as a tool to select a smaller but representative portion of individuals from a larger population for the administration of surveys, whether they are telephone, Internet, face-to-face, or mail surveys. Sampling can also be used in qualitative research as covered in Chapter 6. However, the nature of qualitative research lends itself best to non-probability sampling methods.

The bottom line is that sampling is utilized in a number of different research designs. Although the type of sampling used will vary depending on the goal of the study, sampling does have a place in many research studies in and beyond the social sciences. It is also important to understand that the nature of the research will determine whether the type of sampling required is probability- or non-probability-based sampling. This should become clearer in the sections that examine different types of probability and non-probability samples later in this chapter.

Why Sample?

We’ve hinted at the fact that utilizing a sample can lead to research results that would be similar to results if researchers instead examined the entire population. This is certainly a justification for sampling since it is generally easier and less tedious than utilizing an entire population. For example, consider the study highlighted at the beginning of the chapter where researchers were interested in citizen preferences for rehabilitation versus incarceration for serious juvenile offenders in four different states (Pennsylvania, Washington, Illinois, and Louisiana). The combined population of these four states is just over 35 million individuals. Instead of drawing a sample, suppose the researchers wished to conduct telephone interviews with the entire population of eligible phone numbers in each of these four states. The number of telephone surveys to be conducted among the eligible and participating population would be prohibitive in a number of areas—time, expense, staff needs, and length of time required to complete, analyze, and report results. In short, it would simply not be feasible for a small research team to conduct such a study with an entire population.

The good news is that sampling, under certain conditions, allows researchers to retrieve results from a sample that are similar to the results that would have been obtained by utilizing the entire population. Although there will be some degree of difference between the results produced from a sample compared to an entire population (called sampling error), this error can be estimated and considered. In short, taking a smaller representative sample of a larger population is often as sufficient as surveying or otherwise utilizing the entire population in a research study.

Representativeness and Generalizability

Two foundations of sampling are representativeness and generalizability. This is particularly true when researchers utilize probability sampling methods, because a major goal of probability sampling is that the sample is representative of the larger population. Representativeness is achieved when the sample provides an accurate picture of the larger population. And if the sample represents the larger population, the results from the sample can then be used to make generalizations about the larger population.

Consider a hypothetical population of criminal justice students at a large university. Let’s say the criminal justice student population comprises 2,500 students, half males and half females. Suppose researchers randomly sampled approximately 500 criminal justice students, and 85% of the sample turned out to be males and only 15% females. Based only on gender, it is clear that this sample does not accurately represent the larger population of criminal justice students. Therefore, any results produced from the 500-person criminal justice sample cannot accurately be generalized back to the larger population. In fact, the results produced were almost entirely responses from males. The results may well represent the population of male criminal justice students at the university, but the results would not generalize to all criminal justice students in the population. In sum, samples can only be generalized back to what they represent—in this case, male criminal justice students and not all criminal justice students at the university.

The previous discussion brings up the issue of generalizing to a specific population and that of generalizing results beyond a particular population. If a sample is representative of a specific population, researchers can be confident that the results of a study generalize or apply back to the specific population from which they selected their sample. For example, if the sample of 500 criminal justice students above accurately represented the criminal justice student population by gender, we might say that any results produced from surveying the 500 criminal justice students reflects the results that would have been found by gender if the whole population of 2,500 criminal justice students was surveyed.

Generalizing results from a representative sample to a specific population does not mean that the results automatically generalize to all similar populations. For example, the opinions on carrying personal weapons on campus from a representative sample of criminal justice students at one Texas university may represent well the opinions of all criminal justice students on that campus. But their opinions may be much different from those of students at a university in Iowa, or criminal justice students in Norway. Perhaps the bottom line is that consumers must be attuned to notions of representativeness and generalizability and must be very cautious of research findings that purport to generalize well beyond the specific population and sample utilized in a research study. Only through replication with different samples from varying populations can more confidence be attached to such broad claims of generalizability between different populations.

Sampling Error and Sample Size

Inasmuch as the results from a probability sample are meant to be a close approximation of what would actually be found if an entire population were utilized, there is certain to be some degree of difference in the results produced from a sample compared to a population. For example, survey results from a sample of citizens on attitudes toward rehabilitation versus incarceration will not likely be exactly identical to the overall survey results if an entire state population of citizens was surveyed.

The difference in results or outcomes between a sample and a population is called sampling error. Researchers expect there to be a difference between the sample results and the results from an entire population, even when the sample is representative of the population. The good news is that this margin of error can be estimated and considered in research. For an example, go watch any major news program and be attuned to survey results from national surveys. During election time, for example, major news networks broadcast any number of survey or poll results from random samples of U.S. citizens, often called scientific surveys to denote the samples were randomly chosen, and hence, probability samples of some sort. Results from such polls are usually graphically displayed with bar or pie charts and show the percent of Americans in favor or opposed to a particular candidate or issue. Results are usually accompanied by an indicator, such as “margin of error +/– 3%” or some other variation. Such an indicator means that results can vary up or down three percentage points. For example, suppose a survey of randomly selected citizens revealed a presidential approval rating of 47% with a margin of error +/– 3%. Considering the error or difference produced by utilizing a sample instead of an entire population (+/– 3%), the approval could be as high as 50% or as low as 44%. These statistics noted above are an indicator of sampling error, or the expected difference in results produced by sampling versus surveying the entire U.S. population. In short, we know that there will be some degree of error by using a sample; the major question is how much error. Sampling error gives us that indication.

One of the most important factors related to the degree of sampling error is sample size. A general rule is the larger the sample, the lower the sampling error. This is because as the sample gets larger, it more closely approximates the population, and therefore error or difference between the sample and population decreases. When the sample is equal to the population, the error is zero, because the sample is the population! Conversely, very small samples are less representative of the population, results are less generalizable to the population as a whole, and sampling error is greater. Of course, one must consider that even if an entire population was selected to participate in a survey, some eligible participants would not respond, other persons in the population would be unable to be reached or would be unknown (e.g., homeless individuals), and these issues are relevant to consider in discussions of sample versus population, and sampling error. But as a very general rule, the larger the sample, the less sampling error.

Students often wonder about the appropriate sample size for a particular research study. Based on the previous discussion, it would seem that the larger the sample, the better. This is generally true when considering the notion of sampling error. However, constraints of the research process—high costs, staffing, tight deadlines—might mean that a larger sample is not feasible. Study constraints notwithstanding, there is no clear-cut rule concerning what constitutes the appropriate sample size. Sample size depends on a number of considerations: size of the population, how much variability exists in the population, and demands of certain statistical techniques, among others.

Consider the issue of population variability. Instead of a social science survey, consider how large a sample of the world population we might need to take to determine what a human heart looks like. There are variations in human hearts to be sure based on age and lifestyle and many other considerations, but there is no need to cut into hundreds of people to come to a conclusion of what a human heart looks like. This is because when it comes to human hearts, there is not a lot of variability in the population. Very small samples in this example would suffice and would be representative of the population and therefore generalizable to the population as a whole. The sample size situation is different when we want to ask people their opinions on any number of issues—people who are spread across different cultures and geographies and who each have unique influences and life experiences. As opposed to a human heart, a larger sample is needed because there is much more diversity in the population.

The bottom line is that sample size is less important than obtaining a representative sample. An extremely large unrepresentative sample is much less useful than a more modest sample size that is representative of a particular population. In this way, samples are akin to gifts—bigger is not always better!

Probability Sampling Methods

The key feature that makes probability sampling methods different from non-probability sampling methods lies in how the sample is selected. In probability sampling methods, selection of the sample is accomplished through a random process such that every member of the population has an equal chance at selection for the sample. To ensure that every member of the population has an equal chance at selection, probability sampling techniques require a random and unbiased process for selection. Researchers must have access to a complete listing of the population, also called a sampling frame. In many cases, researchers might not have access to a list of the population. Researchers might also not have the resources, need, or motivation to utilize a complete list of the population, even if it were available. In these cases, non-probability samples are utilized. Such samples are not comprised of individuals with an equal chance at being selected for the sample.

Before delving into the various probability and non-probability sampling techniques, it is important to briefly revisit the notion of representativeness and generalizability. Researchers who are interested in generalizing sample results to a larger population must ensure that the sample is not biased and is an adequate representation of the population. Accomplishing representativeness, and hence generalizability, is the province of probability sampling techniques. The four probability sampling techniques are examined below.

Simple Random Sampling

Simple random samples are simply samples drawn randomly from a larger population. The key to selecting a simple random sample is that every member of the population has an equal chance at being selected for the sample—no one individual or group of individuals has a greater or lesser chance of getting selected than another individual or group of individuals.

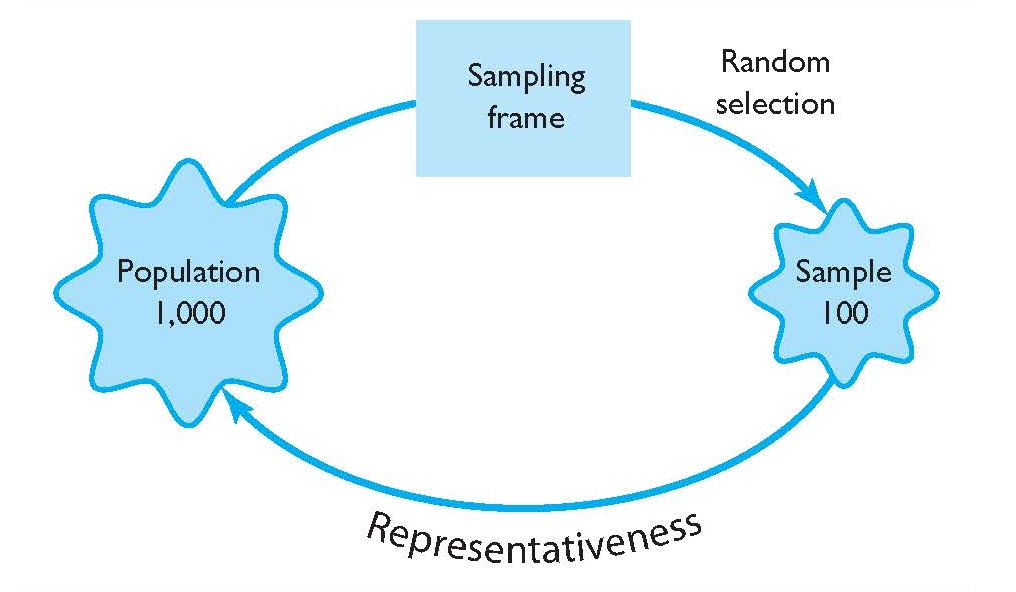
The procedure for drawing a simple random sample is relatively straightforward, as with other forms of probability sampling (see Figure 3.1). First, the researcher must identify the target population from where the sample will be drawn. Selecting a target population is obviously driven by the aim of a particular research study. For example, if a researcher wishes to elicit the opinions of undergraduate criminal justice students at a large southern university, the population would be all undergraduate criminal justice students enrolled at the university. In another example, if the goal is to elicit the opinions of residents in Dade County, Florida, the population would be residents of Dade County, Florida.

Once the target population is identified, the researcher must obtain a listing of the population. Obtaining a listing of the population is one of the more difficult, yet crucial, parts of probability sampling. This list of the population is often called a sampling frame. Because a sampling frame is a list of the population, sampling frames come in many forms. For example, general sampling frames might include phone books, voter registration records, census contacts, or records from the department of motor vehicles. Each of these sampling frames includes members of a certain population, for example, residents of a city or county or other regional indicator. If a researcher wished to survey undergraduate criminal justice students for their opinions on carrying weapons on campus, the sampling frame would be a listing of all criminal justice students—by name or student number or some other indicator.

FIGURE 3.1 | Simple Random Sampling

One crucial consideration involved in the use of a sampling frame is that it be a complete listing of the population. Sampling frames that do not include all members of a target population are problematic. In cases where the sampling frame is incomplete in some way, any samples drawn from the sampling frame may not be truly representative of the population. For example, if a researcher used a phone book as a sampling frame of county residents, there is likely to be a substantial number of members from the population missing because not all residents have phones. In these cases, the true representativeness of the sample could be called into question, and hence, the generalizability of results produced from the sample. Conversely, a target population and sampling frame of all enrolled undergraduate criminal justice students at a particular university is likely to be complete. Nonetheless, an important step in selecting a simple random sample, and all probability samples, is the presence of a complete sampling frame.

Once a sampling frame is identified, the process of selecting a simple random sample requires that members of the population be selected in a way that each member has an equal chance of selection. In essence, members of the population must be selected randomly. There are a number of different ways to draw a random sample—flipping a coin, rolling a die, or using a lottery type machine. Perhaps the most common way of randomly selecting a sample from a population is through the use of a computer program. A variety of statistical software packages exist (e.g., Statistical Package for the Social Sciences [SPSS]) that will randomly draw a sample from an identified list of the population. Note, for example, that the case study that began this chapter was a form of random selection via computer—random digit dialing. As opposed to using a phone book, however, the researchers utilized a computer program that randomly dialed the last four digits of phone numbers in the area codes among the specified states. Such a process means that every member of the population had an equal chance of having their phone number dialed. Unfortunately, those without a phone number could not be considered for the sample.

Whether members of a sample are selected by computer or some other random selection procedure, what can be ensured is that each member of the sample had an equal chance at selection. One problem with simple random samples, however, is that despite being randomly drawn, it cannot be ensured that the sample is representative of the population. In short, just because everyone in the population had an equal chance at being selected does not mean the sample automatically will represent the population. It is possible, for example, that by a chance occurrence the sample could be highly unrepresentative of the population. Consider, for example, the flipping of a coin. It is possible that flipping a regular coin over 100 times could result in the coin landing on heads 100 times, or 85 times, or 75 times—well beyond the 50 times we would expect by probability. Such an imbalance could occur simply by chance. The same problem could occur with simple random sampling. A population of 500 that included 50% males and 50% females could, by chance, result in a simple random sample with highly imbalanced proportions of one gender or the other. For example, a 200-person sample from this population that included 75% males would not be representative of the population—but this could occur, by chance.

In sum, simple random samples ensure that each member has an equal chance at being selected, but such samples do not guarantee representativeness of the population on known categories of information among the population (e.g., race, gender, age). Provided researchers have information on the population, it is possible to examine whether the sample indeed is an accurate reflection of the population. This is only possible on information to which the researchers are privy, however. For example, if researchers did not know the gender breakdown of the entire population, they would not be able to examine whether the sample is truly representative of the population. Because of the potential chance occurrence of nonrepresentativeness posed by simple random samples, researchers might choose to utilize a stratified random sampling technique.

Stratified Random Sampling

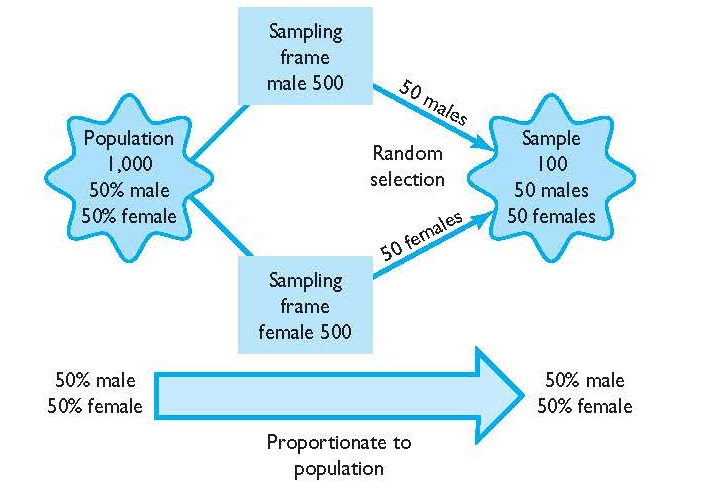
Stratified random sampling is quite similar to simple random sampling (see Figure 3.2 below). The major difference in a stratified sample versus a simple random sample is that the sampling frame is divided up into different strata, based on characteristics of the population. From there, smaller random samples are taken from each strata and then combined into a singular sample. This technique ensures that the final sample is representative of the population based on certain characteristics such as age, race, gender, or whatever is of interest in the research study.

Suppose we wished to conduct a survey on the alcohol drinking behaviors of undergraduates at your college. Let’s say we are most interested in determining whether alcohol consumption differs based upon credit-hour classification: freshman, sophomore, junior, and senior. The population of the college is 4,000 individuals, and we want to take a sample of 100 persons. Based on our knowledge of the population, we know the proportion breakdowns of each classification: freshman (20%), sophomore (25%), junior (25%), and senior (30%). To ensure that our sample of 100 is representative of the population, we first must divide the sampling frame (a list of the student population) into four different strata consistent with the classifications for which we are interested. In essence, we are taking a list of the population of students (the sampling frame), and breaking up this larger sampling frame into four different sampling frames (freshman, sophomore, junior, and senior) to represent each classification. Once we have four sampling frames corresponding to all freshman, sophomores, juniors, and seniors, we then take a random sample from each of the four sampling frames. The size of the random sample from each sampling frame is proportionate to each classification’s proportion of the population. For example, in our desired sample of 100 students, 20 freshman will be randomly selected from the freshman sampling frame, 25 sophomores will be randomly selected from the sophomore sampling frame, 25 juniors, and 30 seniors. This will result in a sample of 100 students, with each classification represented in the sample exactly to their proportion in the population.

FIGURE 3.2 | Stratified Random Sampling (Proportionate)

The process above is an example of proportionate stratified sampling. In proportionate stratified sampling, each predetermined category of the sample (in this case freshman to senior) is represented in the sample exactly proportionate to their percentage of the population. For example, freshman make up 20% of the population, and likewise make up 20% of the final sample. The example above suggests that samples can be stratified based on any number of factors for which researchers have information about the population. For example, the sample could have been stratified by gender and credit-hour classification. To do this, the sampling frame of the entire population would be broken down into multiple sampling frames consistent with gender and classification: freshman women, freshman men, sophomore women, sophomore men, and so on. From there, the sample would simply be randomly selected from each strata, and the number of members in the sample from each strata would be proportionate to their existence in the population. For example, if freshman women make up 10% of the population, and we wish to take a final sample of 100 across gender and classification, 10 freshman women, or 10%, would be included in the final sample. At its essence, stratified sampling is a method researchers use to break down the population into particular sampling frames, and then take a random sample from each sampling frame to create a sample that is perfectly representative of the population (at least on the strata).

As a final note, sometimes researchers are interested in taking a sample from a larger population where one group or strata is overrepresented compared to the group’s proportion of the population. Of course, this smacks against all that has been learned thus far about representativeness. Indeed, in these situations, researchers are actually taking an unrepresentative sample of the population, and they do so on purpose. In some cases researchers do this when a group or strata of interest is so small that drawing a sample proportionate to the group’s membership in the population would result in a sample that is relatively meaningless if comparisons were to be made among other groups. For example, in the hypothetical study on alcohol consumption by credit-hour classification, suppose that freshmen made up only 1% of the population of 4,000 students, sophomores equaled 33%, juniors equaled 33%, and seniors equaled 33%. Among 4,000 students, this would equal only 40 students as the population of freshman. If the population was stratified by classification, and samples proportionate to the population were drawn from those strata, in a 100-person sample, only 1 freshman would be selected. While this 1-person sample would technically represent the proportion of freshmen in the population, this one person would not likely be representative of all 40 freshmen in the population relative to alcohol consumption. What if this one freshman, for example, drank a case of beer a day! This would probably not be an accurate representation of the freshman class. To correct for such extreme imbalances, researchers may oversample the small group, also considered disproportionate stratified sampling. Although it sounds counterintuitive, in some situations researchers must sample in a way that is unrepresentative to ensure adequate representation of a particular group in a sample.

Systematic Random Sampling

Systematic random sampling is another form of probability sampling. Like simple random and stratified random samples, systematic sampling utilizes a random process in the selection of the sample (see Figure 3.3 below). Systematic sampling involves a few basic, but important, steps to ensure that each member of the sample has an equal chance at being selected.

Systematic sampling begins with some sort of list or grouping, and members or items on the list or in the grouping are selected in intervals. The interval is often referred to as taking “every n^th individual.” This means that one portion of selecting the sample entails taking every 5^th, or 6^th, or some other “n^th”.

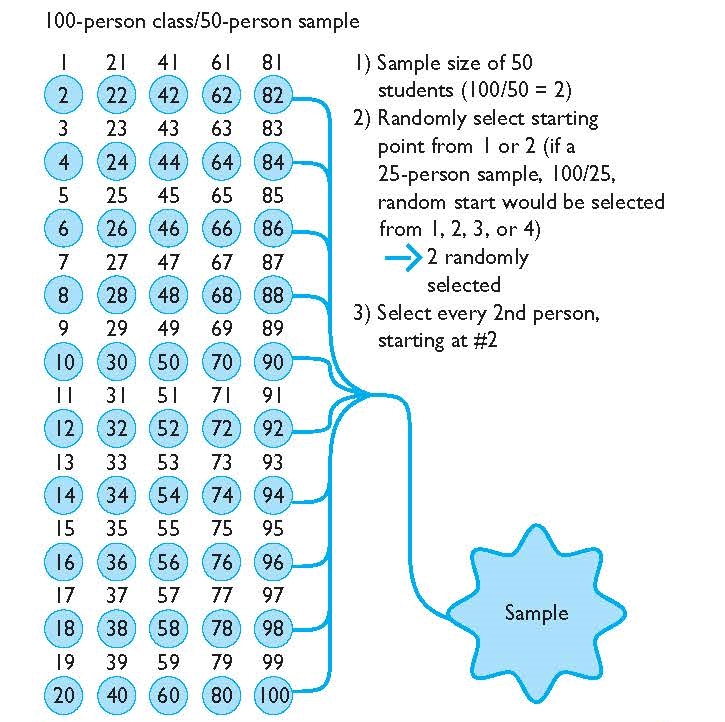
Consider taking a 50-person sample from a 100-person criminal justice class. In this scenario, the professor likely has a list of student names or student ID numbers. Or, the professor could simply line up all the students in front of the class (we are assuming all, of course, are in attendance for a complete population of the class).

Utilizing the student lineup, the professor has to first calculate the sampling interval, or n^th value. To determine this interval, the professor simply divides the population (100) by the number of individuals desired in the sample (50). In this example, the sampling interval is 2 (100/50 = 2). This means every 2^nd person will be selected.

FIGURE 3.3 | Systematic Sampling

The next step to a systematic sample is critical and is what makes it a probability sample. Instead of automatically starting at the top of the list (or front of the lineup), and picking every 2^nd person, the professor must begin with a random starting point. A traditional way to pick a random starting point is to take all of the numbers involved in the interval (1 or 2 in this example), and randomly pick one of the numbers. If the professor picks 1, he or she will start at #1 in the lineup and then take every 2^nd person—1, 3, 5, 7, 9, and so on. If the professor picks 2, he or she will start at #2 and take every second person in the student lineup—2, 4, 6, 8, 10, and so on. An alternative method would be to take 100 numbers, select a number, and then proceed by taking every second person. For example, if the number 6 were chosen, the sample would consist of 6, 8, 10, 12, and so on. In each example, the outcome is essentially the same. In this latter example, once the professor reaches the end of the student lineup, he or she could simply continue selecting every 2^nd person by starting at the beginning of the student lineup until the 50-person sample has been achieved.

By using a random start, the professor ensures that each member of the class population has an equal chance at being selected for the sample. But to further ensure that systematic sampling results in an equal probability of selection, the professor must be sure that the student lineup is not sorted in any particular way that might lead to bias. For example, if the professor sorted the students in such a way that all even-numbered students had the highest class grades and odd-numbered students had the lowest class grades, a resulting sample might be highly biased and not representative of the class as a whole. Such is the case in any form of systematic sampling procedure—it must be ensured that the elements to be sampled are randomly arranged, and do not follow a particular pattern.

Cluster/Multistage Random Sampling

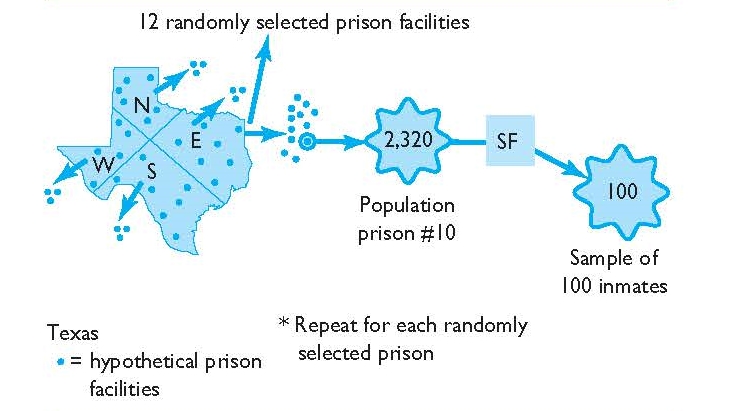
It is sometimes the case that researchers wish to take a sample of individuals dispersed across wide geographical areas. For example, suppose a researcher wanted to conduct a paper-and-pencil survey with a representative sample of 5,000 prison inmates across the sprawling state of Texas. Texas incarcerates more than 150,000 inmates spread across more than 100 incarceration facilities. Because Texas is so large and prison inmates are dispersed all over the state, the thought of drawing a representative sample is a daunting task.

Cluster sampling is a way to narrow down the process of sampling to help ensure that samples are representative of the large population of focus. In this way, cluster sampling first begins by narrowing down large geographic areas—whether they are states, census tracts, or any other large area—into more manageable parts. From there, a series of random samples are drawn of different units, for example, randomly selected prison facilities, randomly selected housing areas within those prison facilities, and finally, randomly selected inmates from the housing areas. The series of random samples implicates the multistage part of cluster/multistage sampling—multiple random samples (see Figure 3.4 below).

Operationally, the first step in the hypothetical prison inmates study would be to narrow down the state of Texas by breaking it down into manageable clusters. Although methods vary, perhaps the state of Texas could be broken down into areas based upon the regions in which prison facilities are located located (or N, S, E, and W as in Figure 3.4). For example, the Texas Department of Criminal Justice is divided into six regions. This could be an initial clustering of the state of Texas. Next, the researcher might obtain a listing of all prison facilities located within each of the six regions. This list serves as a sort of sampling frame. From there, the researcher may choose to draw a simple random sample of five prison facilities in each region, for a total of 30 prison facilities across the state. Note that instead of a simple random sample, the researcher could have stratified the list of prison facilities by any number of measures, such as size, type of inmate population, and so on.

Once the 30 prison facilities are randomly selected, the researcher continues to select random samples. For example, the researcher might obtain a list of all inmates at each of the 30 prison facilities. Once the sampling frame of each facility is obtained, the researcher then selects a random sample of inmates from each facility. In this hypothetical study, this would equal approximately 167 inmates sampled from each of the 30 randomly selected prison facilities for a total of approximately 5,000 inmates.

FIGURE 3.4 | Cluster/Multistage Sampling

As before, any number of steps could be added to the process above. For example, separate housing areas could be randomly sampled within each of the 30 prison facilities. Then, inmates could be randomly chosen from the sampled housing areas. Still further, in each stage, proportionate or disproportionate stratification could occur to help make the sample as representative of the population as possible. As can be seen, cluster/multistage sampling can become tedious. In reality, however, cluster/multistage sampling can be boiled down to the successive drawing of random samples from populations that are large and widely dispersed.

Non-Probability Sampling Methods

As opposed to probability sampling techniques, non-probability samples are not drawn through a random and unbiased procedure. There are many potential reasons that might preclude utilizing a random sample. A main reason is that a ready-made list of the population simply may not be available. For example, suppose a researcher was interested in studying the subculture of hoboes. Although the town of Britt, Iowa, holds the National Hobo Convention each year, there is little in the way of a complete list of hoboes. Moreover, even if Britt kept a list of all hoboes who attend the National Convention, this list would certainly not be complete and capture all hoboes in America. In this situation, the researcher may only have access to a defined number of hoboes. As previously mentioned, a research team may not have the resources, need, or motivation to utilize a complete list of the population, even if it was available. In some cases, those who utilize non-probability sampling techniques are actually interested in a sample that does not necessarily represent some larger population. In these cases, non-probability samples are utilized. Such samples are comprised of individuals from known or unknown populations who did not have an equal chance at being selected for the sample.

At this juncture it is important to note the potential issues faced when members of a particular sample are selected through non-probability sampling methods. Regardless of the reasons for selecting a non-probability sample, the important point to consider is that the resulting sample is likely not representative of a larger population. Absent representativeness, the results generated from a non-probability sample cannot be generalized to a larger population. An examination of different non-probability samples may make it clearer why a researcher might want to utilize these sampling techniques, as opposed to a probability sampling technique.

Convenience Sampling

Perhaps the most basic of all sampling techniques is convenience sampling (also called accidental or haphazard or person-on-the-street sampling). With convenience sampling, individuals in the sample are chosen based on convenience. In this way, it is a form of first-come, first-serve sampling.

Convenience sampling is perhaps the most common form of sampling consumed by the average citizen. Local news casts, for example, that stop people on the street and ask their opinion on any number of topics are typically convenience samples. The advent of the Internet has made surveys based on convenience sampling ever-present. Go visit any 10 websites from sporting websites to governmental research organizations to magazine websites and you are sure to have abundant opportunities to take a survey on any pressing issue. These surveys may come in the form of more aggressive pop-ups, or more passive enticements to complete a survey. Regardless, all of these forms of gathering data are based on convenience sampling—anyone can respond, and usually, multiple times.

The obvious problem with convenience sampling is that it is likely the sample is not representative of the larger population. This does not mean that convenience sampling is not useful. However, if the sample does not represent the population, the results from the sample cannot be generalized to the larger population. This is the critical piece of knowledge that should be understood by research consumers. In many cases, results generated from convenience samples are portrayed to represent the attitudes, opinions, and perspectives of the larger population. This is erroneous. Survey results from a convenience sample, in reality, only represent and hence are generalizable to the sample. For example, suppose a local news crew was on your campus today and stopped 100 students on their way to class to ask their opinions regarding whether students should be able to carry concealed handguns on campus. Suppose the local news crew revealed that 90% of students they surveyed believed that concealed handguns should be allowed on campus. What if 90 out of 100 students who believed guns should be allowed on campus just exited an organizational meeting of a group whose members’ sole purpose is to promote the carrying of weapons on campus. The result from this survey would surely represent the feelings of the convenience sample, but the results might be completely different from students on the campus as a whole if they were instead selected randomly.

Convenience sampling has its uses in the research process. However, results generated from a convenience sample are not likely generalizable to the larger population from which the sample was obtained. As a result, data produced from a convenience sample is quite limited to the specific attributes of the sample and often must be interpreted with some caution.

Purposive Sampling

Purposive sampling (also called judgmental sampling) is aptly named because the researcher is specifically interested in the attributes of the particular sample that was purposely chosen for its characteristics. It is also called judgmental sampling because the researcher is using his or her judgment in selecting a sample that is specific to the goal of the research. A case in point might be the selection of mock jury samples by individuals who work as jury consultants. Jury consultants may, for example, choose members of a sample based on factors such as age, income, education, or anything else that might be useful. Once a particular sample of mock jury members is chosen on these criteria, the jury consultant may present particular pieces of evidence and survey sample members on their feelings toward guilt or innocence at particular phases of evidence presentation. Such consultants might further modify certain variables, such as the method of presentation, the type of presentation, who presents the material, and any other factor so that the jury consultant can examine the impact of these changes on mock juror opinions of guilt and innocence.

In this example, the jury consultant is specifically interested in selecting mock jury members who have particular attributes. Information obtained from a mock jury sample can be used in any number of ways, particularly in voir dire proceedings in which the defense, for example, may attempt to select or strike jurors based on certain characteristics that have been found to influence juror opinions. For example, if through the mock jury trials, high-income individuals were more likely to vote for conviction of a residential burglar than individuals of low income, the jury consultant may recommend to defense lawyers to avoid selecting jurors of a high-income bracket.

No matter how purposive sampling is utilized, the goal of the individual selecting the sample is to be very purposive in selecting the particular sample needed. There is little interest in selecting a representative sample from a larger population; rather, the interest lies in selecting a specific sample that fulfills the goal of the research.

Quota Sampling

Quota sampling is quite similar to convenience sampling. The one major difference is that quota samples are based on some known characteristic of the population. For example, suppose researchers were interested in the opinions of students at a mid-size college on whether students should be allowed to conceal and carry guns on campus. Instead of simply surveying students on a first-come, first-serve basis as in convenience sampling, suppose the researchers were interested in making sure the sample at least reflected the gender composition of the population on campus. For example, at the campus of interest, the student population of 5,000 is evenly split, 50% female and 50% male. The researchers want to take a sample of 100 students. In a quota sample, the researchers will simply ensure that 50 opinion surveys are given to women, and 50 surveys are given to males—largely on a convenience basis. In short, the researchers are interested in obtaining a quota based on the gender composition of the college population.

Although quota sampling is slightly more rigorous than convenience sampling, it is not by much. Despite the fact that researchers are ensuring that the sample is reflective of the proportion of students in the population by gender or some other known characteristic, the sample is still essentially convenience based. As a result, every member of the campus population does not have an equal chance at being selected, and thus, is not representative of the larger college population. Because it is not representative, the results generated from the quota sample do not represent the college population.

Snowball Sampling

Snowball sampling is a non-probability sampling technique utilized when one is attempting to study hard-to-access populations, or more typically, populations whose members are not easily identifiable. For example, there is likely no sampling frame or list (at least not a public one) that contains members of a particular subculture from which to draw a sample. Such groups could range from gang members to those involved in an underground fight club. In a general way, snowball sampling might be considered referral sampling. Because members of a particular population may not be easily identifiable, the researcher attempts to initiate contact with one known member, and through referral, is introduced to subsequent members of the group. Through this referral process, the sample begins to snowball, or grow.

As with all non-probability samples, something to consider with snowball samples is that the end sample may not be representative of the entire population. This is because each member of the population did not have an equal chance at being selected for the sample. In many cases of snowball sampling, the researcher may ultimately only be privy to a small number of members from a larger population. Because representativeness cannot be ensured, neither can generalizability.

Noting the above, recall the many purposes of research: describe, explore, explain, apply, and evaluate. In many cases of non-probability sampling, and specifically with snowball sampling, researchers are interested in exploring a lesser known topic in hopes that future research can delve further. In this way, sometimes non-probability sampling is utilized to provide an overall explanation of a particular area—a sort of starting point on which to build future research efforts.

Chapter Summary

This chapter covered forms of probability and non-probability sampling. Probability sampling is used when the goal of a research study is to obtain an accurate representation of the population for the purposes of generalizability. Whether the population consists of students, city residents, or others, probability sampling techniques ensure that each member of the known population has an equal chance at selection. Simply ensuring that each member of a particular population has an equal chance at selection does not ensure representativeness. And, a representative sample does not ensure results from the sample will generalize to different places and times. However, probability sampling makes achieving the goals of representativeness and generalizability more likely than non-probability samples. Although probability samples are superior to non-probability samples when the goal is representativeness and generalizability, this should not be taken to mean that non-probability samples are not useful in research methods. Non-probability samples—samples in which each member of a particular population does not have an equal chance of selection—are often very useful in particular research studies.

In an overall view, both probability and non-probability sampling techniques should be viewed as a set of tools. Sometimes the right tool is a probability sampling technique, and sometimes the right tool is a non-probability sampling technique. In many cases, the tool used is highly dependent upon the research question that is being asked. Knowing which tool is appropriate to a particular research question is a good step on the path to becoming an informed consumer of research.

Critical Thinking Questions

1. What is the difference between probability and non-probability samples?

2. What are some reasons a researcher would utilize a sample instead of a population?

3. What is sampling error?

4. What is the difference between representativeness and generalizability?

5. What is more important: sample size or representativeness? Explain your thoughts.

Key Terms

cluster/multistage sampling: A type of probability sampling in which large geographical areas are clustered, or divided, into smaller parts. From there, random samples of individuals or groups or locations are taken in successive or multiple steps. For example, breaking a state down into regions would be a form of clustering. From there, taking a simple or stratified or systematic random sample of schools from each cluster would be one stage of sampling. A next stage of sampling might be randomly selecting students from each randomly selected school

convenience sampling: A form of non-probability sampling in which the sample is composed of persons of first contact. Also known as accidental or haphazard sampling, or person-on-the-street sampling

generalizability: In reference to sampling, refers to the ability of the sample findings to generalize or be applied to the larger population. For example, let’s say the findings of a sample survey on attitudes toward the death penalty reveal the majority of the sample is in support of the death penalty. If the sample is a good representation of the population, the results from this survey can be generalized or applied to the population

non-probability sampling methods: As opposed to probability sampling methods, non-probability sampling methods include those sampling techniques in which every member of the population does not have an equal chance at being selected for the sample

population: A population is a complete group. A population could be all students at a university, all members of a city, or all members of a church. A defining feature of a population is that it be complete

probability sampling methods: As opposed to non-probability sampling methods, probability sampling methods include those sampling techniques where every member of the population has an equal chance at being selected for the sample. Such procedures increase the probability that the sample is representative of the population, and hence, that the results produced from the sample are generalizable to the population

proportionate stratified sampling: A sampling method in which each predetermined category of the sample is represented in the sample exactly proportionate to their percentage or fraction of the total population

purposive sampling: As a non-probability sample, purposive sampling involves the researcher selecting a specific or purposeful sample based on the needs of the research. If a researcher was interested in the techniques of residential burglars, their sample would be focused only on such burglars

quota sampling: Similar to convenience sampling, quota sampling does involve taking into account a known characteristic of the population. For example, if 50% of the population is female, and the researcher wants a 100-person sample to survey, the researcher must survey exactly 50 females in a quota sample. Once the quota of 50 females is met, no other females will be surveyed

random digit dialing: A sampling process involving phone numbers where a computer randomly dials the last 4 digits of a telephone number in a given area code using a known prefix. Random digit dialing, in this way, can help remedy the problem of unlisted phone numbers or numbers for which there is no so-called phone book (e.g., cell phones)

randomly drawn sample: A sample for which each member of the population has an equal chance at being selected. Samples not drawn through a random process are those in which each member of the population does not have an equal chance at being selected for the sample

representativeness: In probability sampling processes, representativeness occurs when the smaller sample is an accurate representation of the larger population

sample: A sample is a smaller part of a population

sampling: The process of selecting a smaller group from a larger group. In probability sampling, for example, a smaller group or sample of individuals is taken from the larger group or population. The goal is that the smaller sample accurately represents the population, despite being smaller in number

sampling error: The percentage of error or difference in using a sample instead of an entire population

sampling frame: A complete list of the population that the researcher will use to take a sample. If the sampling frame does not include each member of the population, and hence is not complete, a researcher must question how those who are listed on the sampling frame differ from those who are not accounted for on the sampling frame

simple random samples: As a form of probability sampling, simple random samples are samples randomly drawn from a larger population. Although each member of the population has an equal chance at being selected for the sample, this form of sample cannot guarantee representativeness

snowball sampling: A non-probability sampling technique utilized when a researcher is attempting to study hard to access populations. It is also referred to as referral sampling. In snowball sampling a researcher makes a contact, and that contact refers another, and so on. After time, the sample snowballs or gets larger. Because there is no ready to use sampling frame for some populations (e.g., gang members), researchers must use contacts and referrals to get a sample

stratified random sampling: Stratified sampling is a form of probability sampling where several simple random samples are taken from a population that has been divided up into strata, such as age, race, gender, or any number of strata based on information about the population

systematic random sampling: Systematic random sampling involves selecting every nth person (e.g., 5th, 10th, etc.) from a list. To be considered a probability sample, the starting point on the list must be chosen at random

target population: The population of interest for a particular research study (e.g., all prison inmates, all domestic violence arrestees)

Endnotes

1 Piquero, A., and L. Steinberg. (2010). “Public preferences for rehabilitation versus incarceration of juvenile offenders.” Journal of Criminal Justice, 38, 1–6.

2 Nagin, D., A. S. Piquero, E. S. Scott, and L. Steinburg. (2006). “Public preferences for rehabilitation versus incarceration of juvenile offenders: Evidence from a contingent valuation survey.” Criminology and Public Policy, 5, 301–326.

3 Wright, R., S. H. Decker, A. K. Redfern, and D. L. Smith. (1992). “A snowball’s chance in hell: Doing fieldwork with active residential burglars.” Journal of Research in Crime and Delinquency, 29, 148–161.

4 Vogt, W.P. (1993). Dictionary of statistics and methodology: A nontechnical guide for the social sciences. Newbury Park, CA: Sage, p. 200.